首页 JavaSE

# 前言

集合类是 Java 中非常重要也是最常用的一块，它其实和数学中的定义差不多，是为了更好的管理和操作数据而存在的，前面一部分会先记录一下数据结构的部分，比较偏理解的东西，如果学习过可以跳过这部分，本篇中所有代码都在 Clown_java/src/main/java/JavaSE at master・clown-q/Clown_java (github.com)

# 数据结构

# 顺序表

顺序表存储数据的单元还是数组，不过其数据排列紧凑，物理和逻辑上都是连续的，因为我之前学的数据结构是 c 语言版（当然也学的并不好，不然我也不会在这里记录这样的一篇，感谢老师的不杀之恩），这里可能会贴一些 java 的代码

public class SequenceTable<T> {
    int size = 0;   // 顺序表中当前元素数量
    int max = 10;   // 顺序表能存放的最大元素数量
    Object[] arr = new Object[max];     // 实际存放元素的数组
}

这里定义了一个类，使用泛型可以使得存放的数据更加灵活

# add

public void add(T t,int index){ //T 是要插入的数据，index 是要插入的位置
        if(index<0||index>size){ // 这里判断传入的位置是否合法
            throw new IndexOutOfBoundsException("插入位置不合法,插入的位置只能是0 - "+size);
        }else if(size+1>max){// 判断表是否已满
            throw new IndexOutOfBoundsException("最多只能存放"+max+"个数据，请尝试删除数据后再插入");
        }else {
            for (int i =size;i>index;i--){
                arr[i] = arr[i-1];
            }
            arr[index]=t;
            size++;
        }
    }

这里对于顺序表中的数据满了的策略是抛出异常，当然这里也可以扩充顺序表，也不用手动的回收，这点显然比 C 实现要更加灵活

public void add(T t,int index){ //T 是要插入的数据，index 是要插入的位置
    if(index<0||index>size){
        throw new IndexOutOfBoundsException("插入位置不合法,插入的位置只能是0 - "+size);
    }else if(size+1>max){
        max = max + (max >> 1);
        Object[] arr2 = new Object[max];
        System.arraycopy(arr,0,arr2,0,size);
        arr = arr2;
    }else {
        for (int i =size;i>index;i--){
            arr[i] = arr[i-1];
        }
        arr[index]=t;
        size++;
    }
}

简单的测试一下

public class DataTest {
    public static void main(String[] args) {
        SequenceTable<String> sequenceTable =new SequenceTable();
        for (int i = 0; i<15; i++) {
            sequenceTable.add("aa", 0);
        }
        System.out.println(sequenceTable);
    }
}

image-20230726115440728

# remove

接下来简单写一下删除

public void remove(int index){// 返回删除的元素
        if(index<0||index>size-1){
            throw new IndexOutOfBoundsException("删除的索引不合法,范围应该为0 - "+(size-1));
        }else {
            for(int i=index;i<size;i++){
                arr[i]=arr[i+1];
            }
            size--;
        }
    }

这里也测试一下

public class DataTest {
    public static void main(String[] args) {
        SequenceTable<Integer> sequenceTable =new SequenceTable();
        for (int i = 0; i<15; i++) {
            sequenceTable.add(i, 0);
        }
        System.out.println(sequenceTable);
        sequenceTable.remove(4);
        System.out.println(sequenceTable);
    }
}

image-20230726120537963

# getIndex

然后是取指定位置的元素，这个就比较简单，直接检查一下索引，合法就输出就行

public void getIndex(int index){
        if(index<0||index>size-1){
            throw  new IndexOutOfBoundsException("索引不合法,范围应该为0 - "+(size-1));
        }else {
            System.out.println(arr[index]);
        }
    }

简单的验证一下

public class DataTest {
    public static void main(String[] args) {
        SequenceTable<Integer> sequenceTable =new SequenceTable();
        for (int i = 0; i<15; i++) {
            sequenceTable.add(i, 0);
        }
        System.out.println(sequenceTable);
        sequenceTable.remove(4);
        System.out.println(sequenceTable);
        sequenceTable.getIndex(3);
    }
}

image-20230726122100487

还有一些别的功能，比较简单，这里就不在写了

# 链表

上面的顺序表实际上还是数组，而链表不在使用数组，通过 “指针” 来连接各个结点，物理上不相邻，逻辑上是相邻的，又分为两种，带头结点和不带头结点的两种结构

带有头结点的结构，头结点中不存放数据

常用的是带头结点的链表

image-20230726140247231

public class LinkedList<T> {
    class Node<T>{// 结点
        private T data; // 结点存放的数据
        private Node<T> next; // 指向下一个结点
        public Node(T data) {
            this.data = data;
        }
    }
    private Node<T> headNode = new Node<>(null);// 头结点设置为空
    private int size=0;
}
这样就定义好了一个链表，存放数据的是内部类 Node 中的 data 成员属性，使用 next 做一个链接
# add
链表的插入和顺序表是不同的效率较高
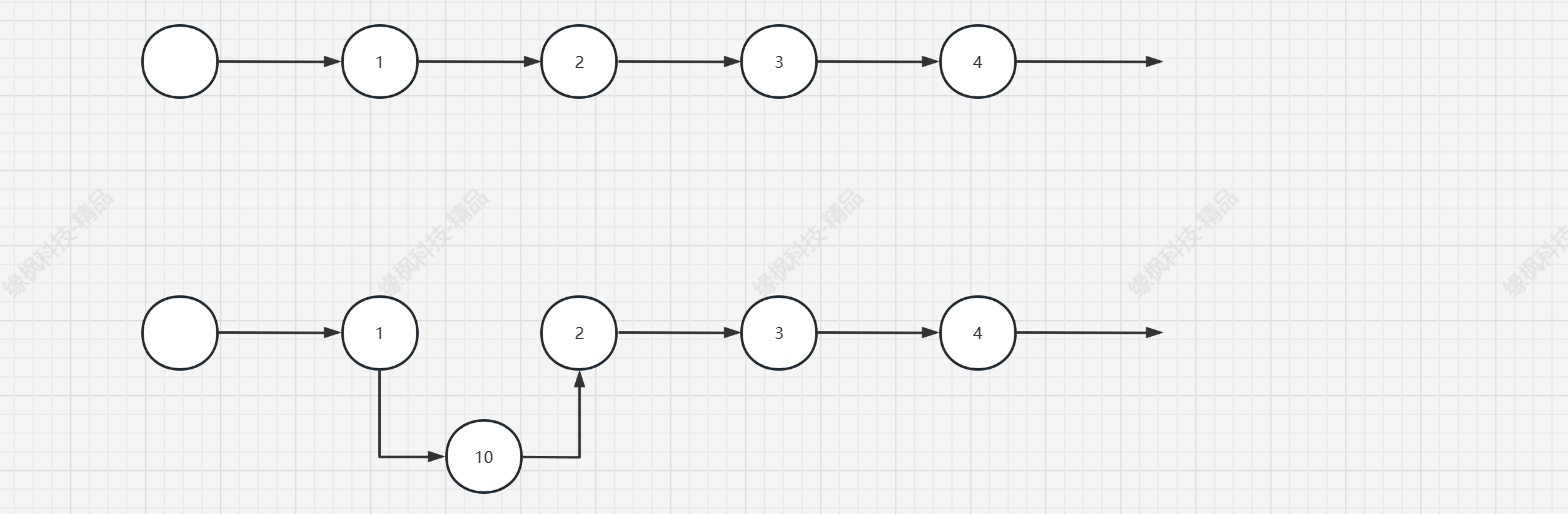
image-20230726140727682
像上图中，想要将 10 插入到 1 和 2 之间，首先将 1,2 之间的连接断开，1 指向 10,10 指向 1 就完成了插入，接下来看看代码是怎么实现的
public void add(T t,int index){
        if(index<0||index>size){
            throw new IndexOutOfBoundsException("插入位置不合法,插入的位置只能是0 - "+size);
        }else {
            Node<T> head = headNode; // 使用头结点
            for (int i = 0;i<index;i++){
                head = head.next; // 遍历到要插入的位置
            }
            Node<T> node = new Node<>(t); // 创建一个新的结点
            node.next = head.next; // 新结点指向当前结点指向的结点
            head.next = node; // 前一个结点指向当前结点
            size++;
        }
    }
这里重写本类和内部类的 toString 方法
public class LinkedList<T> {
    class Node<T>{// 结点
        private T data; // 结点存放的数据
        private Node<T> next; // 指向下一个结点
        public Node(T data) {
            this.data = data;
        }
        @Override
        public String toString() {
            return "Node{" +
                    "data=" + data +
                    ", next=" + next +
                    '}';
        }
    }
    private Node<T> headNode = new Node<>(null);// 头结点设置为空
    private int size=0;
    public void add(T t,int index){
        if(index<0||index>size){
            throw new IndexOutOfBoundsException("插入位置不合法,插入的位置只能是0 - "+size);
        }else {
            Node<T> head = headNode; // 使用头结点
            for (int i = 0;i<index;i++){
                head = head.next; // 遍历到要插入的位置
            }
            Node<T> node = new Node<>(t); // 创建一个新的结点
            node.next = head.next; // 新结点指向当前结点指向的结点
            head.next = node; // 前一个结点指向当前结点
            size++;
        }
    }
    @Override
    public String toString() {
        return "LinkedList{" +
                "headNode=" + headNode +
                ", size=" + size +
                '}';
    }
}
写一个测试方法
public static void main(String[] args) {
        LinkedList<Integer> linkedList = new LinkedList<>();
        linkedList.add(1,0);
        linkedList.add(1,0);
        System.out.println(linkedList);
    }
image-20230726142510718
可以看见，这里添加方法就写好了
# remove
接下来就是删除方法
image-20230726142927765
还是这样一个链，比如说想删除 2，现将 1 直接指向 3 就可以了
public void remove(int index){
        if(index<0||index>size-1){
            throw new IndexOutOfBoundsException("删除的索引不合法,范围应该为0 - "+(size-1));
        }else {
            Node<T> head = headNode;
            for(int i=0;i<index;i++){
                head=head.next;
            }
            head.next=head.next.next;
            size--;
        }
    }
这个就比较简单，测试类中这样写
public static void main(String[] args) {
        LinkedList<Integer> linkedList = new LinkedList<>();
        for (int i = 0; i<3; i++) {
            linkedList.add(i, 0);
        }
        System.out.println(linkedList);
        linkedList.remove(1);
        System.out.println(linkedList);
    }
image-20230726143443895
这里有回收机制，不用管空出来的结点 2
# getindex
获取对应位置上的数据
public void getIndex(int index){
        Node<T> head = headNode;
        for(int i=0;i<index;i++){
            head = head.next;
        }
        System.out.println(head.data);
    }
遍历到，然后直接获取即可，测试方法
public static void main(String[] args) {// 链表
        LinkedList<Integer> linkedList = new LinkedList<>();
        for (int i = 0; i<5; i++) {
            linkedList.add(i, 0);
        }
        System.out.println(linkedList);
        linkedList.remove(1);
        System.out.println(linkedList);
        linkedList.getIndex(3);
    }
image-20230726143930080
顺序表支持随机访问，读取数据的速度较块，但是插入删除时效率低，而链表刚好相反，所以根据需求选择合适的数据结构更好
# 栈
一种特殊的顺序表，只能在表尾操作，不能直接操作前面的参数，先进后出的一种数据结构，可以基于之前的顺序表和链表，不过有两种写的功能
  • pop，出栈，从栈顶取一个元素
  • push，入栈，从栈顶加入一个元素
或许你会注意到这里有一个新的词，栈顶，前面说我们只能在表尾部操作，尾部这一端通常我们称为栈顶，另一端称为栈底
简单来说，就是有限制的线性表，这里选用链表来实现一下
public class Stack_Linked<T> {
    class Node<T>{
        T data;
        Node<T> next;
        public Node(T data) {
            this.data = data;
        }
        @Override
        public String toString() {
            return "Node{" +
                    "data=" + data +
                    ", next=" + next +
                    '}';
        }
    }
    private Node<T> nodeHead = new Node<>(null);
    private int size = 0;
    public void push(T t){
        Node<T> node = new Node<>(t);// 创建一个新结点
        node.next = nodeHead.next; // 新结点指向头结点指向的结点
        nodeHead.next=node; // 头结点指向新结点
        size++;
    }
    public T pop(){
        if (nodeHead.next==null){ // 判断栈空
            throw new NoSuchElementException("栈是空的");
        }
        T t = nodeHead.next.data; // 保存数据
        nodeHead.next = nodeHead.next.next; // 头结点指向下一个结点的下一个结点
        size--;
        return t;
    }
    @Override
    public String toString() {
        return "Stack_Linked{" +
                "nodeHead=" + nodeHead +
                ", size=" + size +
                '}';
    }
}
这样就实现了一个简单的栈，写一个测试方法
public static void main(String[] args) {// 栈
        Stack_Linked<Integer> stackLinked = new Stack_Linked<>();
        stackLinked.push(10);
        stackLinked.push(10);
        stackLinked.push(10);
        System.out.println(stackLinked);
        stackLinked.pop();
        System.out.println(stackLinked);
    }
image-20230726161401532
# 队列
前面记录了栈，它是一种特殊的线性表，有着先进后出的性质，其实是一种有限制的线性表，而队列也差不多，它就和他的名字队列一样，队头的先操作，不能插队
元素只能在队尾插入，只能从队首出队，先进先出
队列也是可以使用链表和顺序表两种来实现，这里还是使用链表
image-20230726163059182
大概是上图这种结构
public class Queue_Listed<T> {
    private class Node<T>{
        T data;
        Node<T> next;
        public Node(T data) {
            this.data = data;
        }
        @Override
        public String toString() {
            return "Node{" +
                    "data=" + data +
                    ", next=" + next +
                    '}';
        }
    }
    private Node<T> nodeHead = new Node<>(null);// 头结点，指向队首
    private int size = 0;
    @Override
    public String toString() {
        return "Queue_Listed{" +
                "nodeHead=" + nodeHead +
                ", size=" + size +
                '}';
    }
}
这里和链表的结构相同，多定义了一个尾结点
# add
public void add(T t){
        Node<T> head = nodeHead;
        for (int i=0;i<size;i++){ // 找到尾结点
            head = head.next;
        }
        Node<T> node = new Node<>(t); // 创建新结点
        head.next = node;
        size++;
    }
写一个测试方法
public static void main(String[] args) {
        Queue_Listed<Integer> queueListed =new Queue_Listed<>();
        queueListed.add(10);
        queueListed.add(10);
        queueListed.add(10);
        System.out.println(queueListed);
    }
image-20230726164213140
# remove
public T remove(){
        T t = nodeHead.next.data;
        if (nodeHead.next==null){
            throw  new NoSuchElementException("队列为空");
        }
        nodeHead.next = nodeHead.next.next;
        size--;
        return t;
    }
这里将队首的指向的数据返回，首接结点指向下一个结点的下一个结点，写一个测试方法
public static void main(String[] args) {
        Queue_Listed<Integer> queueListed =new Queue_Listed<>();
        queueListed.add(10);
        queueListed.add(10);
        queueListed.add(10);
        System.out.println(queueListed);
        System.out.println(queueListed.remove());
        System.out.println(queueListed);
    }
image-20230726164834586
# 二叉树
前面都是线性表的的数据结构，下面开始树型结构的记录，树型结构名副其实，它和树一样，从一个点有多个分结点，各个分节点不相交
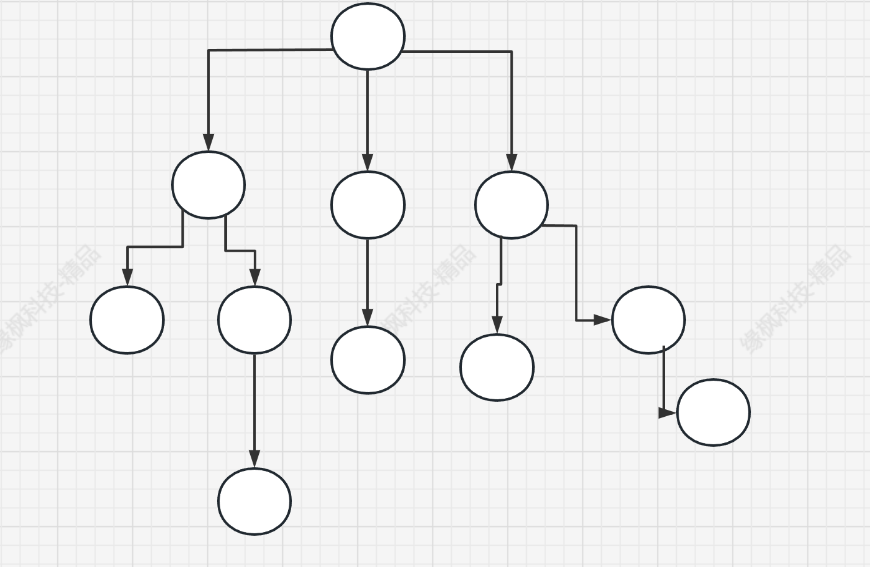
image-20230726165708337
类似于这种结构，这里简单的记录一下树的相关概念：
  • 根节点，上图中最上方这个节点称为根节点，就和树根一样
  • 度，一个结点其子结点的个数
  • 树的深度，整个树的最大层数
  • 一个结点下面的直接相连的结点被称为子结点
  • 没有子结点的结点被称为叶子结点
  • 同一个结点的子结点之间互相为兄弟节点
而二叉树是度为 2 的树，接下来看代码实现
二叉树中的结点的子树是有左右之分的
public class BinaryTree<T> {
    public T data;
    public BinaryTree<T> left,right;
    public BinaryTree(T data) {
        this.data = data;
    }
}
因为二叉树的最大度是 2，所以这里有两个引用就可以了
这里建立一个如下图的二叉树
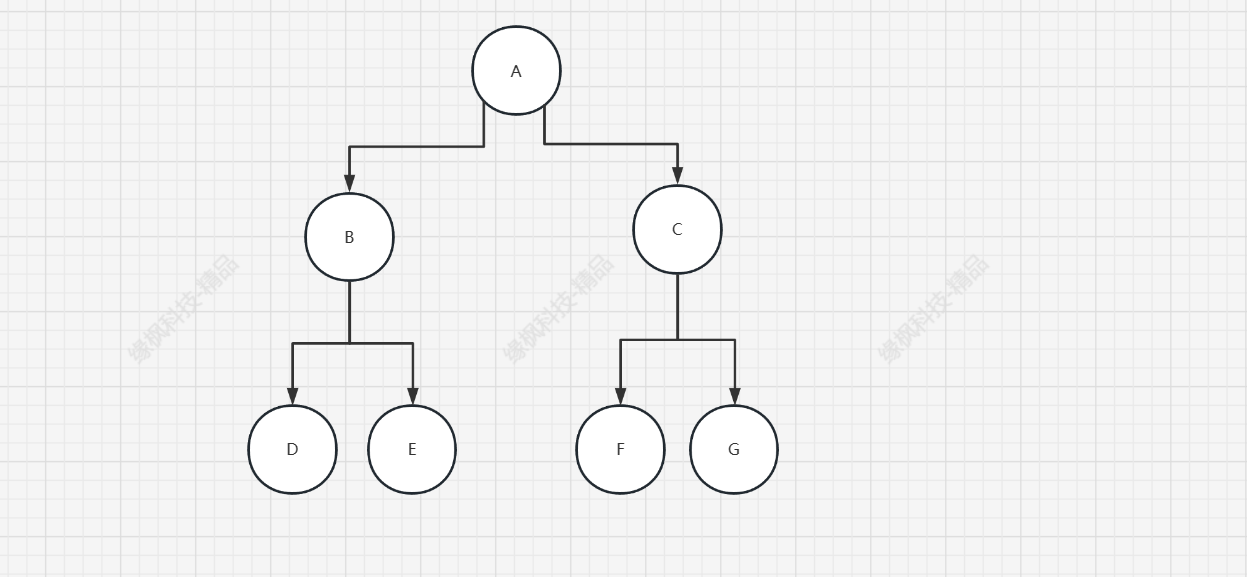
image-20230726172949239
public static void main(String[] args) {
        BinaryTree<Character> binaryTree1 = new BinaryTree<>('A');
        BinaryTree<Character> binaryTree2 = new BinaryTree<>('B');
        BinaryTree<Character> binaryTree3 = new BinaryTree<>('C');
        BinaryTree<Character> binaryTree4 = new BinaryTree<>('D');
        BinaryTree<Character> binaryTree5 = new BinaryTree<>('E');
        BinaryTree<Character> binaryTree6 = new BinaryTree<>('F');
        BinaryTree<Character> binaryTree7 = new BinaryTree<>('G');
        binaryTree1.left = binaryTree2;
        binaryTree1.right = binaryTree3;
        binaryTree2.left = binaryTree4;
        binaryTree2.right = binaryTree5;
        binaryTree3.left = binaryTree6;
        binaryTree3.right = binaryTree7;
    }
# 集合类
也是正式开始集合类的学习，集合和数组差不多，表示一组对象，集合为了更加方便的管理数据，但是他们还是有很多不同之处
  • 集合是可变的，而数组的大小在定义的时候就已经固定了
  • 数组只能存放一种数据，而集合可以存放不同的数据类型
  • 集合只能是引用类型，也就是说只能存放对象
# 集合根接口
其实这些集合类都是 jdk 已经实现好了的
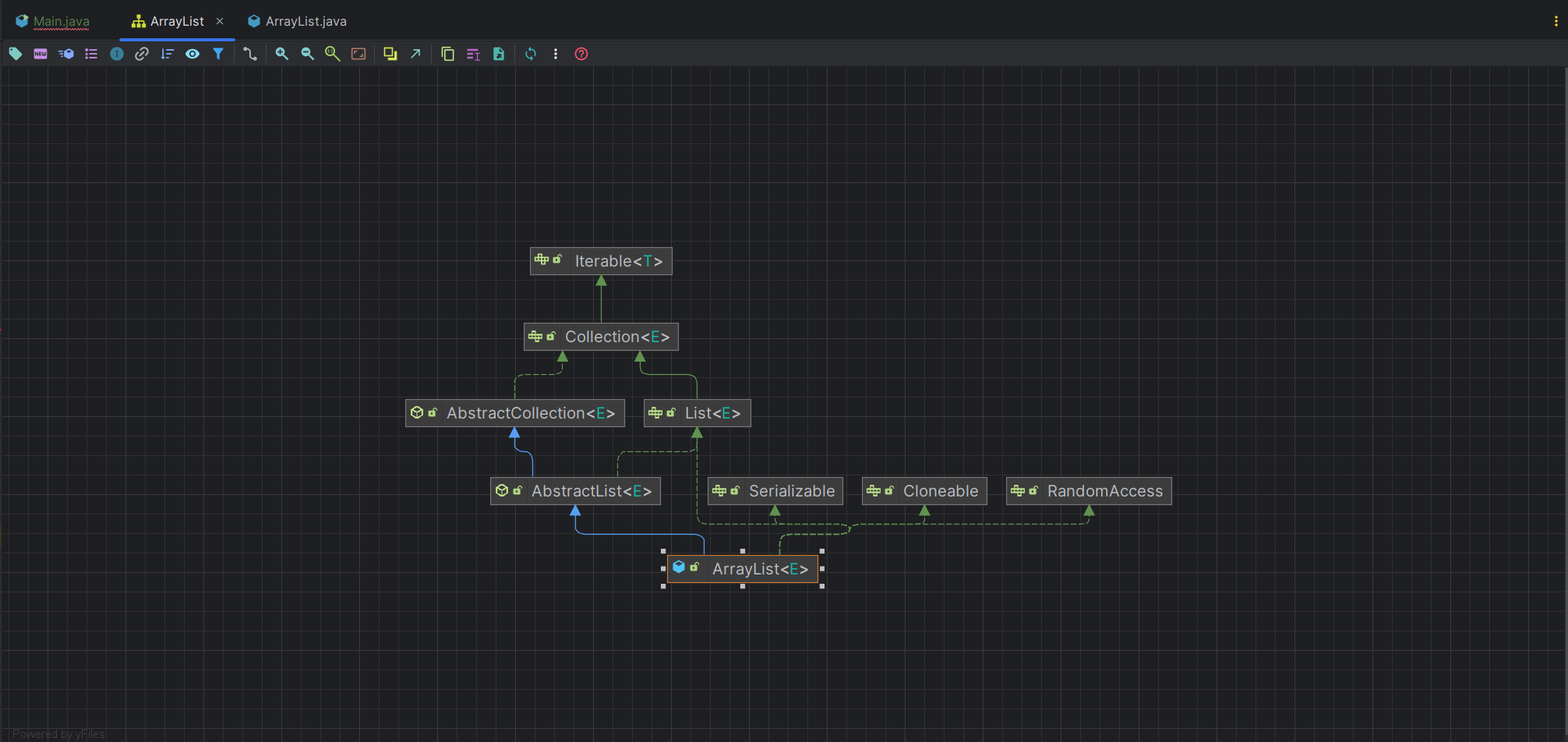
image-20230726184508009
这里看一下 ArrayList 的继承关系，也可以去看源码
image-20230726184608134
这里 Lterable 是迭代器，实际上的接口其实是 Collection，详细看一下这个接口
image-20230726184945963
可以看到，它是集合层次结构中的根接口，这里简单看一下，都有哪些方法
int size(); // 集合中元素数量
	boolean isEmpty();// 判断集合是否为空
	boolean contains(Object o); // 判断集合是否包含某个元素
    
	Iterator<E> iterator(); // 生成当前集合的一个迭代器
    Object[] toArray(); // 转化为对应的数组，默认转化为 Object
    <T> T[] toArray(T[] a); // 提供一个类型
    boolean add(E e);  // 添加数据到集合
    boolean remove(Object o); // 从集合中删除元素
    boolean containsAll(Collection<?> c);  // 判断是否包含子集
    boolean addAll(Collection<? extends E> c);  // 添加集合中的所有元素
    boolean removeAll(Collection<?> c); // 删除给定集合中的所有元素
    default boolean removeIf(Predicate<? super E> filter);	// 更具条件移除元素
    
	boolean retainAll(Collection<?> c); // 保留给定集合中的元素
    void clear();  // 清空集合
    boolean equals(Object o);  // 判断两个集合是否相等
    int hashCode(); // 计算集合的 hash 值
实际上学习集合这块内容主要是看各个实现类是怎么做的，理解一下东西比较多，但是不难
# List 列表
list 其实就是前面写到的线性表，其实也是一个接口，存放数据的地方是一个可扩容的数组，他其实与顺序表差不多，元素通过下标访问，可以有重复的元素
集合中判断是否为重复的元素，使用的是 equals 方法来判断
public class Main {
    public static void main(String[] args) {
        ArrayList<Integer> arrayList = new ArrayList<>();
        arrayList.add(10);
        System.out.println(arrayList.contains(10));
    }
}
比如说，这段代码实例化一个集合后，向其中插入一个元素 10，然后通过 contains 判断
image-20230726192525849
这里是返回 true 的，那么我再向集合中加入一个元素 10
public class Main {
    public static void main(String[] args) {
        ArrayList<Integer> arrayList = new ArrayList<>();
        arrayList.add(10);
        System.out.println(arrayList.contains(10));
        arrayList.add(10);
        System.out.println(arrayList);
    }
}
image-20230726192638181
这里可以看到是可以的
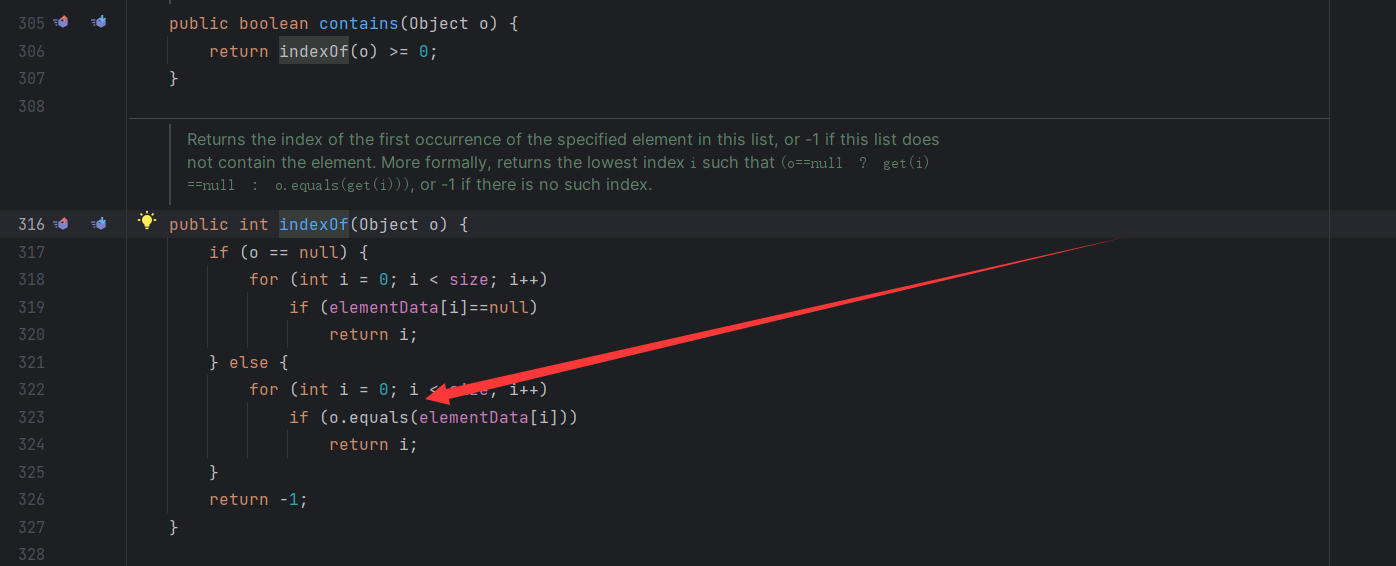
image-20230726192808736
可以看到其实这是使用的是 equals 判断的
# ArrayList
这里看一下 ArrayList 上的实现思路
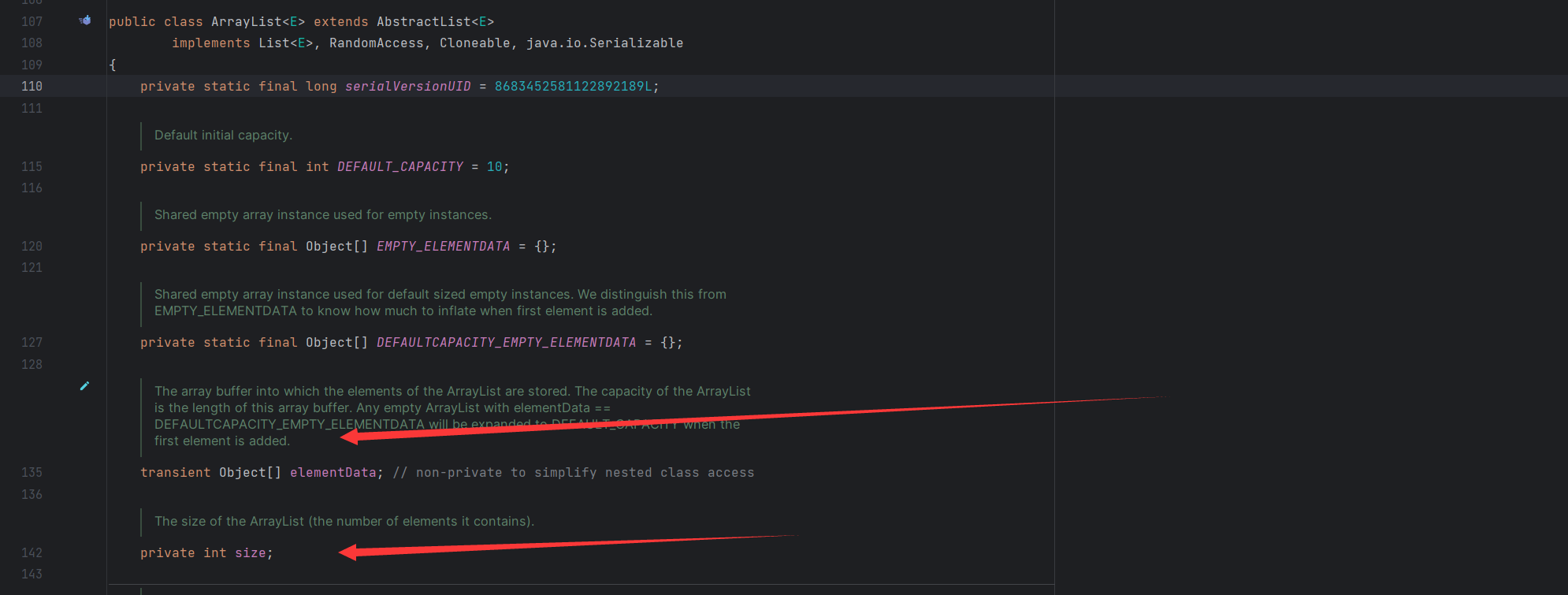
image-20230726194559821
前面也说过它实际上是通过数组来存储数据，这里也可以证明，同样用了一个 size 存储大小
image-20230726194726734
如果不带参数，回默认创建一个长度为零的数组
image-20230726194857588
当然也可以自定义初始化长度
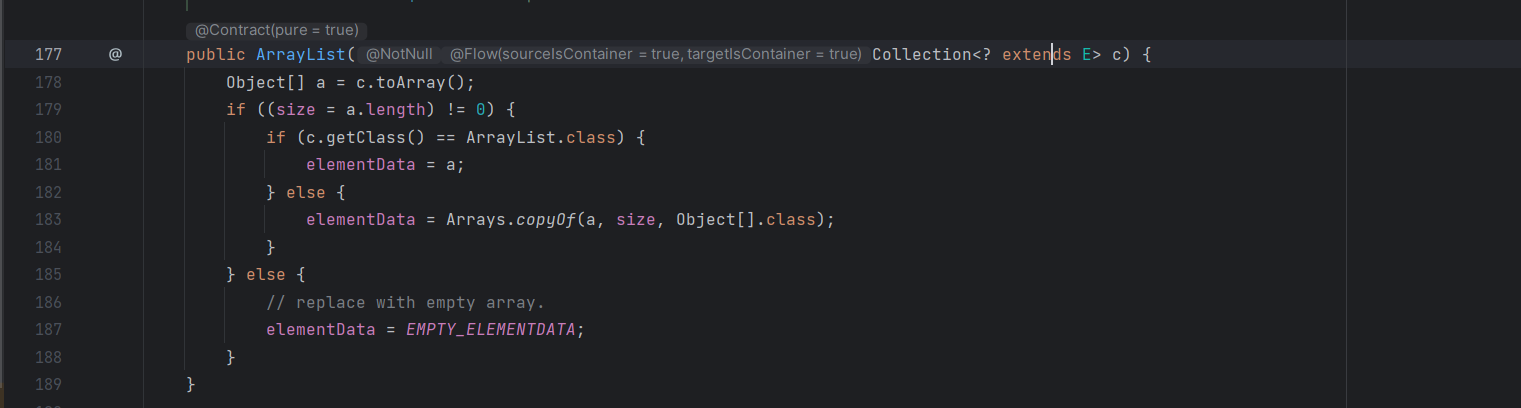
image-20230726194932324
也可以直接通过一个集合去创建另一个集合
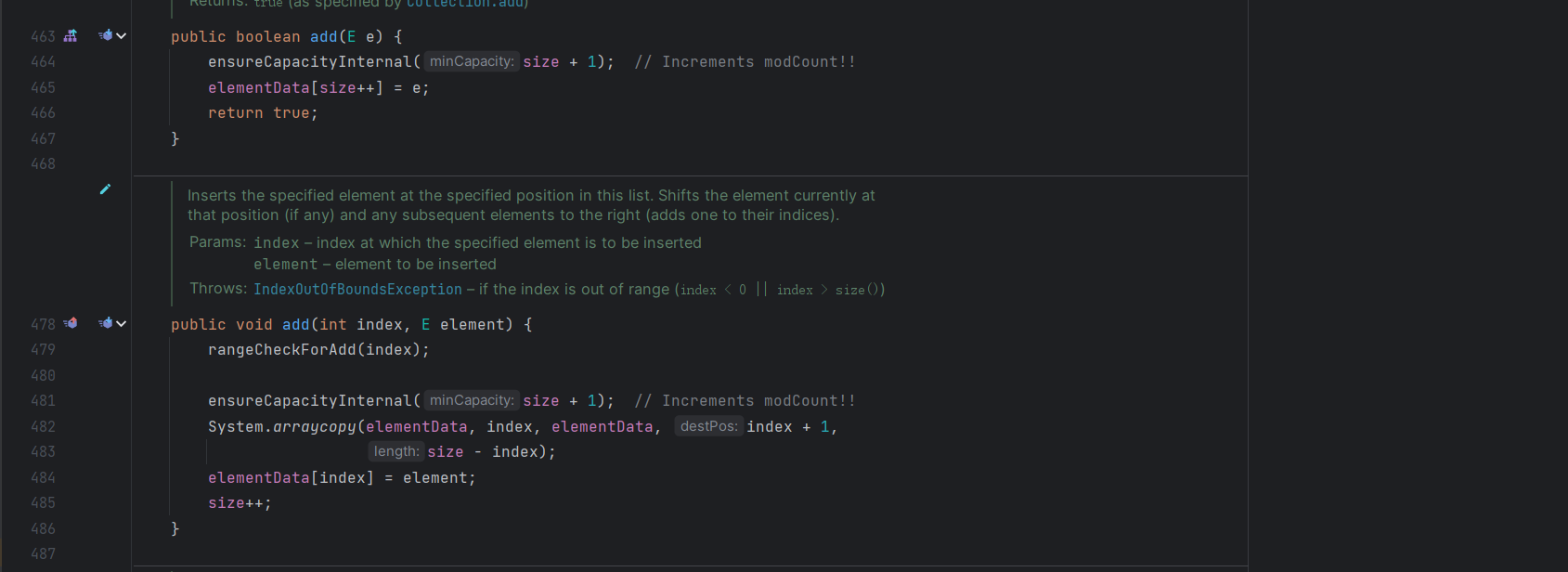
image-20230726195037353
先看一下 add 的方法其实这里和我之前在数据结构部分的实现逻辑是一样的
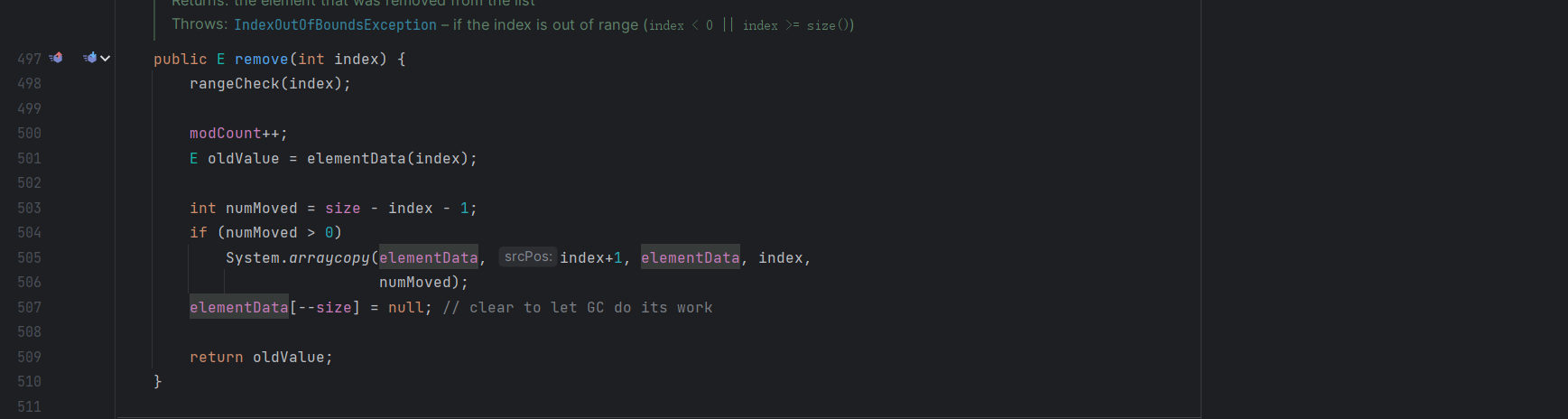
image-20230726200543379
接着看一下 remove 方法，先检查范围
image-20230726200622317
然后通过 elementData 获取元素，然后使用 arraycopy 将元素进行一个复制，这个方法效率更高，但是逻辑还是一样的
实现原理不太一样，但是功能其实和 ArrayList 是一样的
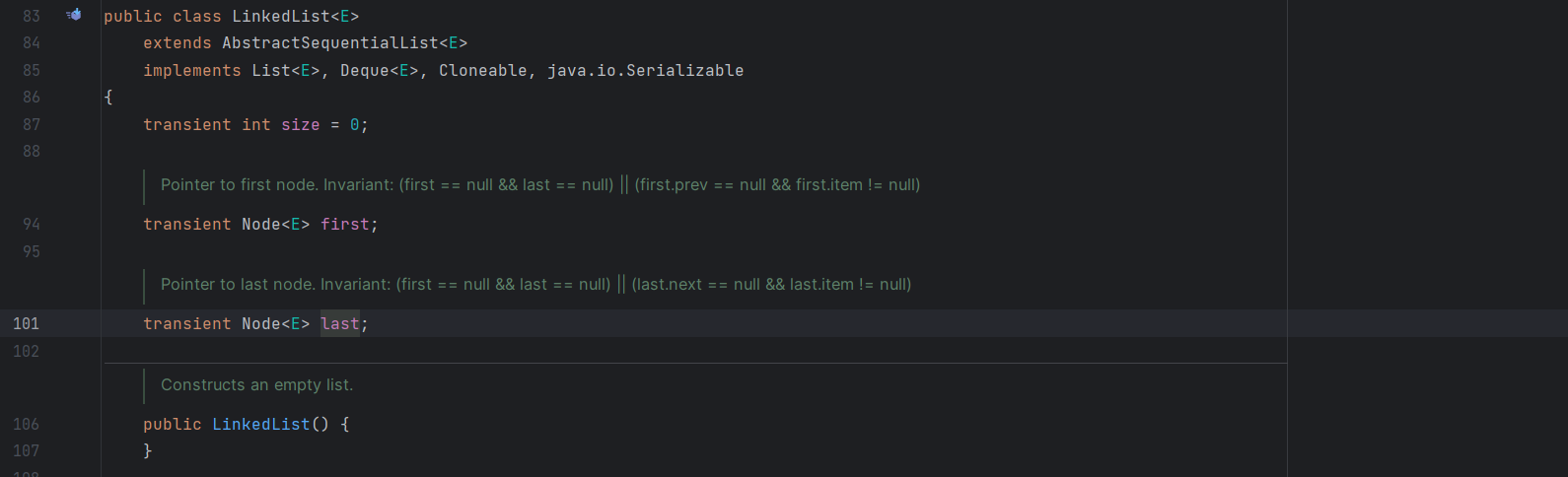
image-20230726203800294
这里它只有三个成员变量，大小，第一个结点，最后一个结点
image-20230726203823562
它存放数据是这样的一个结点，使用的是一个双向链表
他的 add 方法
image-20230726204025801
这里直接调用了 linkLast
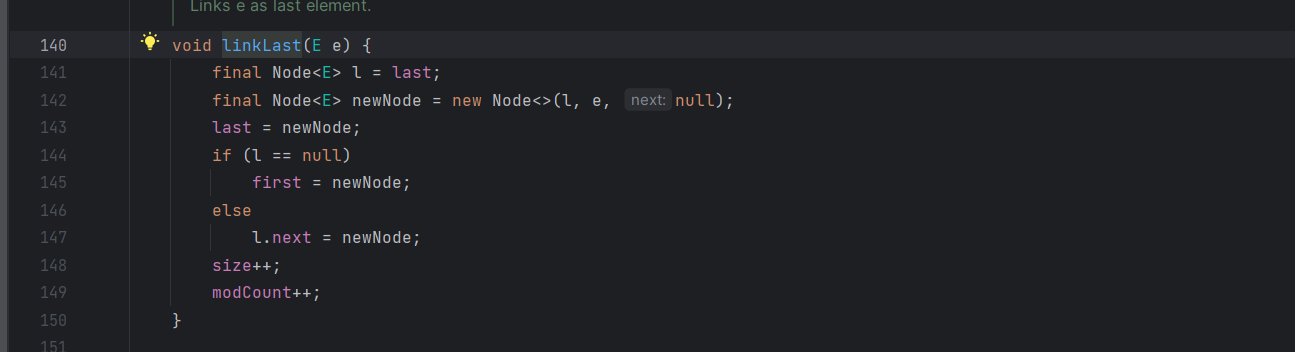
image-20230726204051426
逻辑还是一样的，不过这里是双向链表，还是有点区别的
# Set 集合
set 集合是一种保证没有重复元素的集合
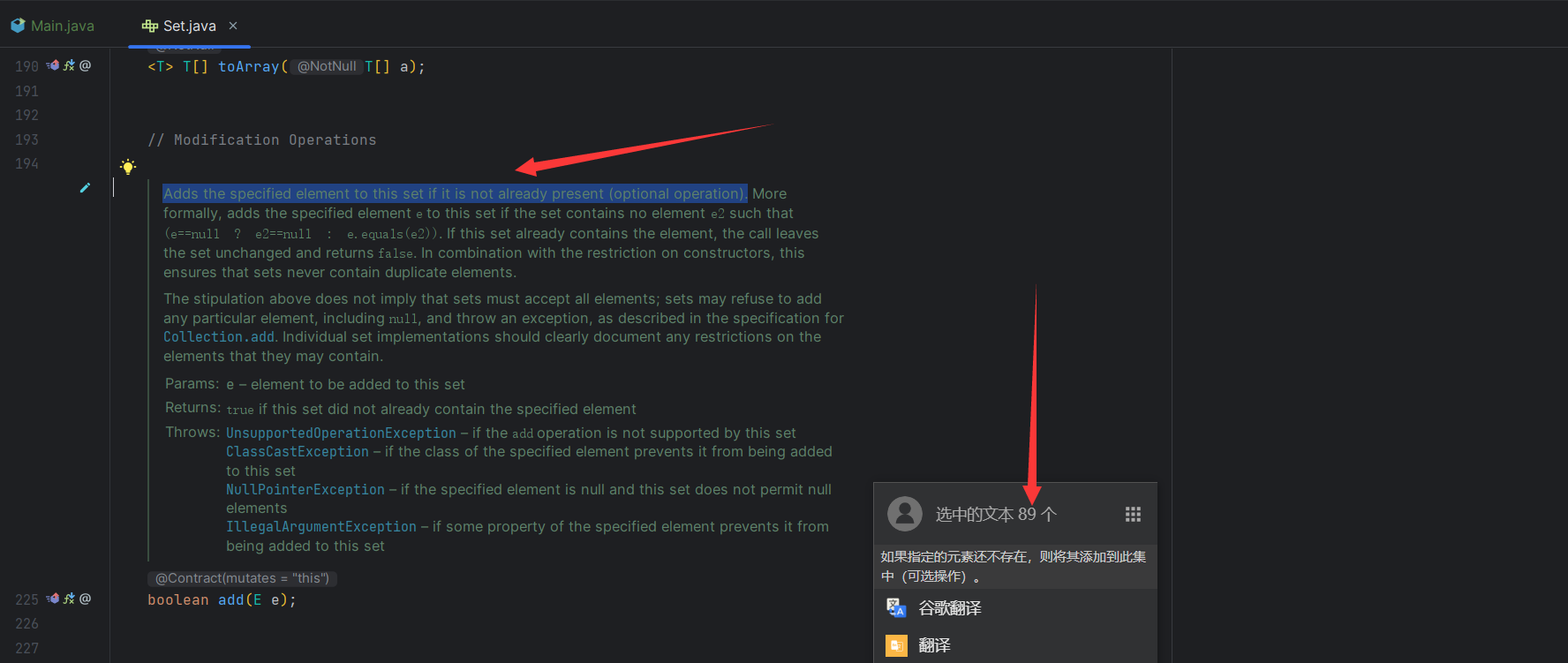
image-20230727074328198
这点可以从 add 方法中体现出来，其他的方法都是 Collection 接口中继承过来的，这里还是具体看一下实现类
# HashSet
这里实际上是一个 HashMap 在实现
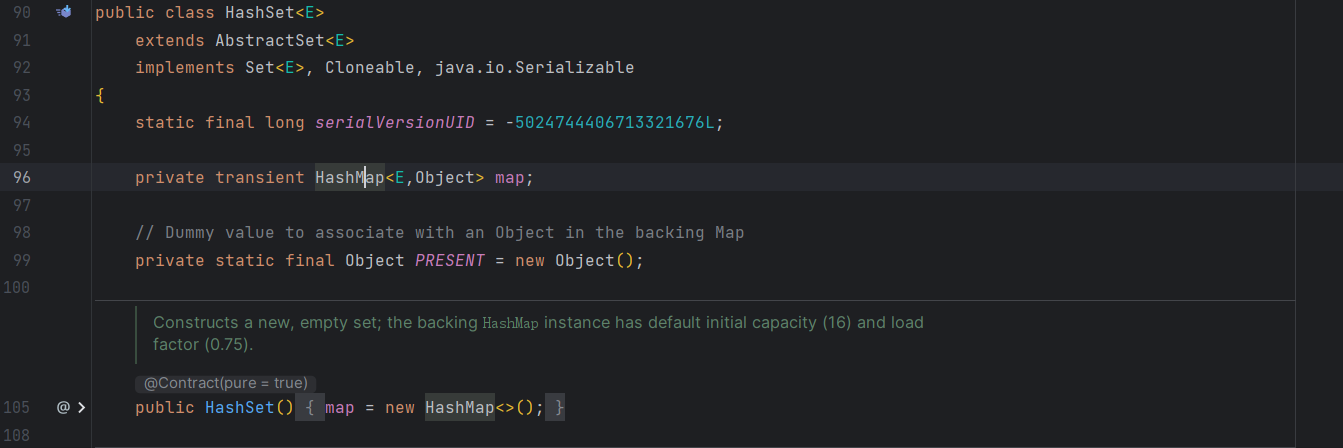
image-20230727074739525
这里会在后面 map 的记录中再详细的看一下，先看看常用的一些方法
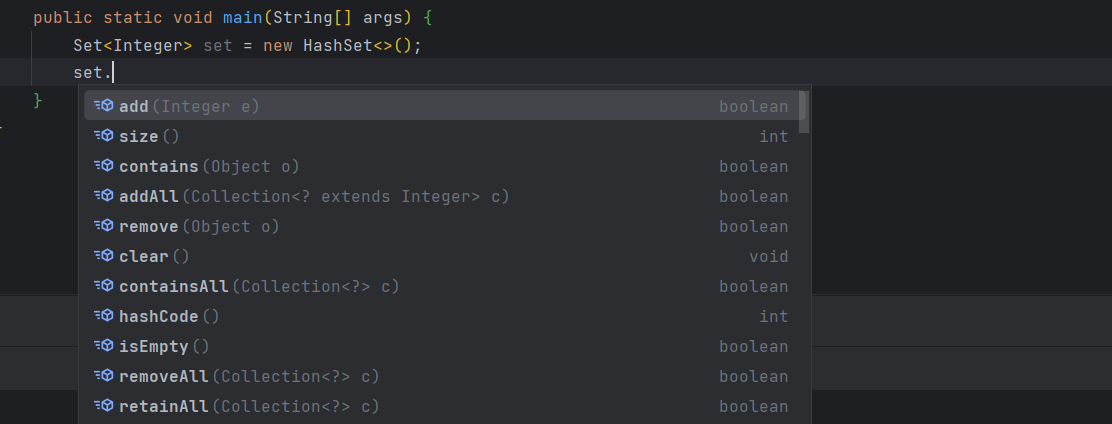
image-20230727074856320
这里可以看到有的方法很多，这里先尝尝添加两个相同的元素
public static void main(String[] args) {
        Set<Integer> set = new HashSet<>();
        System.out.println(set.add(10));
        System.out.println(set.add(10));
        System.out.println(set);
    }
image-20230727075029615
这里可以看到，第二次添加实际上是失败了的
# Map 映射
映射简单来说，就是两个元素之间的对应关系，而在 Map 中这种关系被存储为键值对
image-20230727080712044
它有着这样一个限定，这实际上很 “映射”
image-20230727080839710
Map 和之前不同的是，他并没有继承 Collection 接口，这里举例一个最简单的使用
public static void main(String[] args) {
        Map<Integer,String> map = new HashMap<>();
        map.put(1,"test1");
        map.put(2,"test2");
        System.out.println(map.get(2));
    }
image-20230727085646500
其他使用的方法很多，但是很简单，这里不在一一列举
在 HashMap 中存放数据的地方实际上
image-20230727095011322
这里其实很简单的逻辑，存放 hash，key，value，指向 next
image-20230727095528744
存放 hash 表的地方，这里就是一个最核心的地方，接着简单的看一下 put 方法
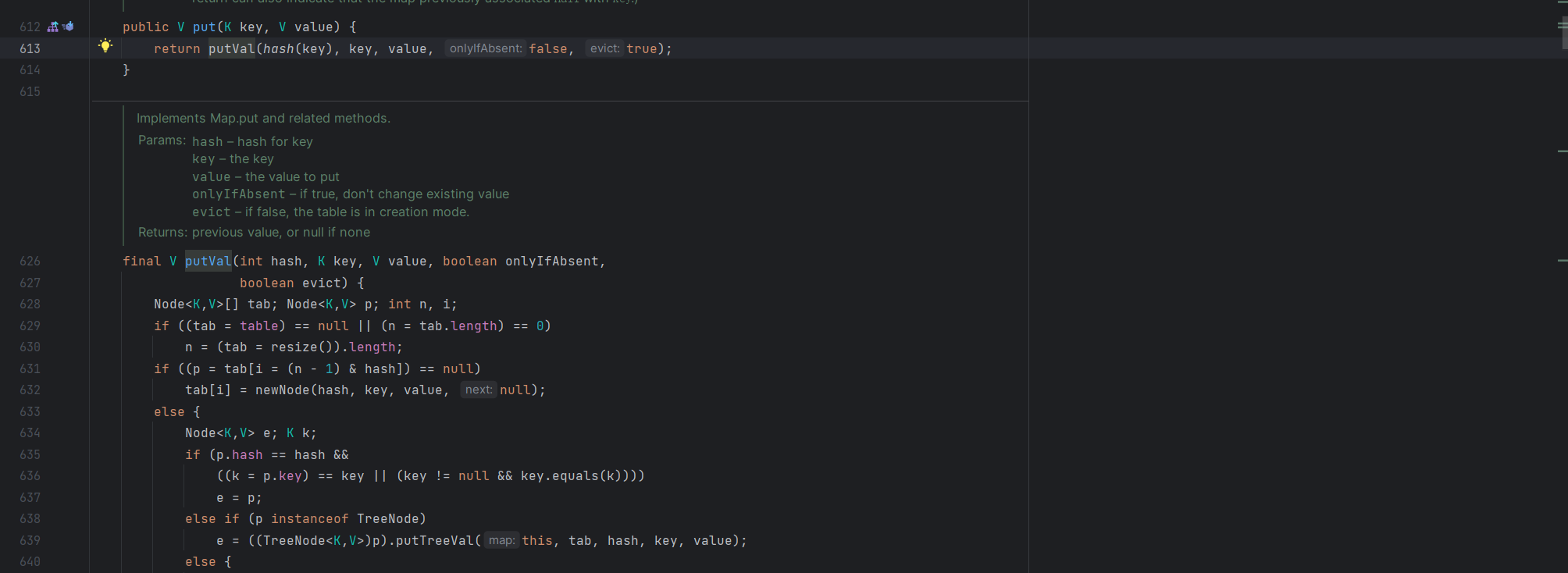
image-20230727095918747
这里可以看到 put 方法将 key 值 hash 后一并传入 putVal 方法，这个代码块比较长，这里我加了一下注释可以看一下
final V putVal(int hash, K key, V value, boolean onlyIfAbsent, boolean evict) {
    Node<K, V>[] tab; // 哈希表数组
    Node<K, V> p; // 表示要插入的位置处的节点
    int n, i; // 数组长度 n，计算插入位置的索引 i
    // 如果哈希表数组为空或长度为 0，则初始化
    if ((tab = table) == null || (n = tab.length) == 0)
        n = (tab = resize()).length;
    // 根据 hash 值计算插入位置的索引
    if ((p = tab[i = (n - 1) & hash]) == null)
        tab[i] = newNode(hash, key, value, null); // 如果该位置为空，直接插入新节点
    else {
        Node<K, V> e; // 用于遍历链表或树的节点
        K k; // 临时保存节点的键
        // 判断第一个节点是否与要插入的键相同
        if (p.hash == hash && ((k = p.key) == key || (key != null && key.equals(k))))
            e = p; // 如果相同，将 p 节点作为要插入的位置
        else if (p instanceof TreeNode)
            e = ((TreeNode<K, V>) p).putTreeVal(this, tab, hash, key, value); // 如果是树节点，调用树节点的插入方法
        else {
            // 遍历链表，查找是否已经存在相同的键
            for (int binCount = 0; ; ++binCount) {
                if ((e = p.next) == null) {
                    // 如果遍历到链表末尾仍未找到相同键，则在链表末尾插入新节点
                    p.next = newNode(hash, key, value, null);
                    if (binCount >= TREEIFY_THRESHOLD - 1) //-1 为了保持链表结构
                        treeifyBin(tab, hash); // 判断是否需要将链表转换为树
                    break;
                }
                // 判断链表中是否存在相同的键
                if (e.hash == hash && ((k = e.key) == key || (key != null && key.equals(k))))
                    break;
                p = e; // 继续遍历链表
            }
        }
        if (e != null) { // 存在相同的键，更新值
            V oldValue = e.value;
            if (!onlyIfAbsent || oldValue == null)
                e.value = value;
            afterNodeAccess(e); // 节点访问后的处理，用于 LinkedHashMap 等特殊处理
            return oldValue; // 返回旧的值
        }
    }
    ++modCount; // 哈希表修改次数加 1
    if (++size > threshold)
        resize(); // 判断是否需要调整哈希表大小
    afterNodeInsertion(evict); // 节点插入后的处理，用于 LinkedHashMap 等特殊处理
    return null; // 返回 null 表示插入的键之前不存在于哈希表中
}